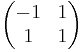Weighing matrix
In mathematics, a weighing matrix W of order n with weight w is an n × n 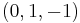 -matrix such that
-matrix such that 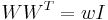 . A weighing matrix is also called a weighing design. For convenience, a weighing matrix of order
. A weighing matrix is also called a weighing design. For convenience, a weighing matrix of order  and weight
and weight  is often denoted by
is often denoted by 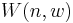 .
.
A 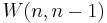 is equivalent to a conference matrix and a
is equivalent to a conference matrix and a 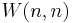 is an Hadamard matrix.
is an Hadamard matrix.
Some properties are immediate from the definition:
- The rows are pairwise orthogonal.
- Each row and each column has exactly
 non-zero elements.
non-zero elements. 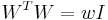 , since the definition means that
, since the definition means that 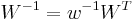 (assuming the weight is not 0).
(assuming the weight is not 0).
Example of W(2, 2):
The main question about weighing matrices is their existence: for which values of n and w does there exist a W(n,w)? A great deal about this is unknown. An equally important but often overlooked question about weighing matrices is their enumeration: for a given n and w, how many W(n,w)'s are there? More deeply, one may ask for a classification in terms of structure, but this is far beyond our power at present, even for Hadamard or conference matrices.
External links
- On Hotelling's Weighing Problem, Alexander M. Mood, Ann. Math. Statist. Volume 17, Number 4 (1946), 432-446.